Equations of Motion:

First equation of motion:

By definition, Acceleration

= Change in velocity / Time

= (Final velocity – Initial velocity)/Time

= (OC – OD) / OE

= DC / OE

a = DC / t

DC = AB = at

From the graph EB = EA + AB

v = u + at

This is the first equation of motion.

Second equation of motion:

From the graph the distance covered by the object during time, t is given by the area of quadrangle DOEB

s = Area of the quadrangle DOEB

= Area of the rectangle DOEA + Area of the triangle DAB

= (AE × OE) + (1/2 × AB × DA)

s = ut + ½ at²

This is the second equation of motion.

Third equation of motion:

We see that the distance covered by the object during time, t is given by the area of the quadrangle DOEB.

Here, DOEB is a trapezium. Then,

s = Area of trapezium DOEB

= ½ × Sum of length of parallel side × Distance between parallel sides

= ½ × (OD + BE) × OE

s = ½ × (u + v) × t

Since, a= (v – u) / t or t = (v – u)/a

s = ½ × (v + u) × (v – u)/a

2as = v² – u²

v² = u² + 2 as

This is the third equation of motion.

The Motion of an Object Falling Freely on Its Own:

• You can observe that, both the stone and the eraser reach the surface of the earth almost at the same time.
• When you drop the eraser and paper, the eraser reaches first and the sheet of paper reaches later.
• You can also observe that the paper crumpled into a ball reaches ground first and plain sheet of paper reaches later, although they have equal mass.
• Do you know the reason? When all these objects are dropped in the absence of air medium (vacuum), all would have reached the ground at the same time.
• In air medium, air offers some resistance to the motion of freely falling objects.
• But, it is negligibly small when compared to the gravitational pull acting on the stone and rubber.
• Hence, they reach the ground at the same time.
• It can be seen from these activities that the magnitude of air resistance depends on the area of objects exposed to air.
• We know that an object experiences acceleration during free fall.
• This acceleration experienced by an object is independent of mass.
• This means that all objects hollow or solid, big or small, should fall at the same rate.
• The equation of motion for a freely falling body can be obtained by replacing ‘a’ in equations with g, the acceleration due to gravity.
• For a freely falling body which is initially at rest, u = 0.
• Thus, we get the following equations.

v = gt, s = ½ gt² , v² = 2gh

• When we throw an object vertically upwards, it moves against the acceleration due to gravity.
• Hence, ‘a’ is taken to be –g and when moving downwards ‘a’ is taken as +g.

Newton’s laws of motion:

Newton’s First Law:

• This law states that everybody continues to be in its state of rest or the state of uniform motion along a straight line unless it is acted upon by some external force.
• It gives the definition of force as well as inertia.

Newton’s Second Law of Motion:

• According to this law, “the force acting on a body is directly proportional to the rate of change of linear momentum of the body and the change in momentum takes place in the direction of the force”.
• This law helps us to measure the amount of force.
• So, it is also called as ‘law of force’.
• Let, ‘m’ be the mass of a moving body, moving along a straight line with an initial speed ‘u’ After a time interval of ‘t’, the velocity of the body changes to ‘v’ due to the impact of an unbalanced external force F.

Initial momentum of the body Pi = mu

Final momentum of the body Pf = mv

Change in momentum Δp = P_f –P_i

= mv – mu

By Newton’s second law of motion,

Force, F ∝ rate of change of momentum

F ∝ change in momentum / time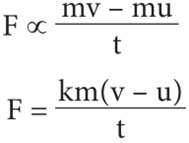

Here, k is the proportionality constant.

k = 1 in all systems of units. Hence,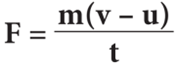

Since, acceleration = change in velocity/ time, a=(v-u)/t. Hence, we have

F = m × a

Force = mass × acceleration

• No external force is required to maintain the motion of a body moving with uniform velocity.
• When the net force acting on a body is not equal to zero, then definitely the velocity of the body will change.
• Thus, change in momentum takes place in the direction of the force.
• The change may take place either in magnitude or in direction or in both.
• Force is required to produce the acceleration of a body.
• In a uniform circular motion, even though the speed (magnitude of velocity) remains constant, the direction of the velocity changes at every point on the circular path.
• So, the acceleration is produced along the radius called as centripetal acceleration.
• The force, which produces this acceleration is called as centripetal force.

Units of force: SI unit of force is newton (N) and in C.G.S system its unit is dyne.

Definition of 1 newton (N): The amount of force required for a body of mass 1 kg produces an acceleration of 1 m s^–2, 1 N = 1 kgms^–2

Definition of 1 dyne: The amount of force required for a body of mass 1 gram produces an acceleration of 1 cm s ^–2, 1 dyne = 1 gcms ^–2; also 1 N = 105 dyne.

Unit force: The amount of force required to produce an acceleration of 1 ms^–2 in a body of mass 1 kg is called ‘unit force’.

Gravitational unit of force:

• In the SI system of units, gravitational unit of force is kilogram force, represented by kg f.
• In the CGS system its unit is gram force, represented by g f.

1 kgf = 1 kg × 9.8 ms^-2 = 9.8 N;

1 gf = 1 g × 980 cms^-2 = 980 dyne

Newton’s Third Law of Motion:

• Newton’s third law states that ‘for every action, there is an equal and opposite reaction.
• They always act on two different bodies’.
• If a body A applies a force F_A on a body B, then the body B reacts with force F_B on the body A, which is equal to F_A in magnitude, but opposite in direction.

F_B = –F_A

Examples:

• When birds fly they push the air downwards with their wings (Action) and the air pushes the bird upwards (Reaction).
• When a person swims he pushes the water using the hands backwards (Action), and the water pushes the swimmer in the forward direction (Reaction).
• When you fire a bullet, the gun recoils backward and the bullet is moving forward (Action) and the gun equalises this forward action by moving backward (Reaction).

Impulsive force:

• A large force acting for a very short interval of time is called as ‘Impulsive force’.
• When a force F acts on a body for a period of time t, then the product of force and time is known as ‘impulse’ represented by ‘J’.

Impulse, J = F × t

By Newton’s second law

F = Δp / t (Δ refers to change)

Δp = F × t

J = Δp

• Impulse is also equal to the magnitude of change in momentum. Its unit is kgms^–1 or Ns.
• Change in momentum can be achieved in two ways.

They are:

• A large force acting for a short period of time and
• A smaller force acting for a longer period of time.

Examples:

• Automobiles are fitted with springs and shock absorbers to reduce jerks while moving on uneven roads.
• In cricket, a fielder pulls back his hands while catching the ball.
• He experiences a smaller force for a longer interval of time to catch the ball, resulting in a lesser impulse on his hands.

The Principle of Rocket Launch:

• Propulsion of rockets is based on the law of conservation of linear momentum as well as Newton’s III law of motion.
• Rockets are filled with a fuel (either liquid or solid) in the propellant tank.
• When the rocket is fired, this fuel is burnt and a hot gas is ejected with a high speed from the nozzle of the rocket, producing a huge momentum.
• To balance this momentum, an equal and opposite reaction force is produced in the combustion chamber, which makes the rocket project forward.
• While in motion, the mass of the rocket gradually decreases, until the fuel is completely burnt out.
• Since, there is no net external force acting on it, the linear momentum of the system is conserved.
• The mass of the rocket decreases with altitude, which results in the gradual increase in velocity of the rocket.
• At one stage, it reaches a velocity, which is sufficient to just escape from the gravitational pull of the Earth. This velocity is called escape velocity.

State Newton’s law of general gravitation and its applications:

• This law states that every particle of matter in this universe attracts every other particle with a force.
• This force is directly proportional to the product of their masses and inversely proportional to the square of the distance between the centers of these masses.
• The direction of the force acts along the line joining the masses.
• Force between the masses is always attractive and it does not depend on the medium where they are placed.
• Let, m₁ and m₂ be the masses of two bodies A and B placed r meter apart in space

Force                               F ∝ m₁ × m₂

F ∝ 1/ r²

• On combining the above two expressions
  
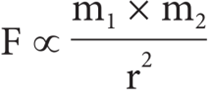
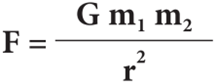
• Where G is the universal gravitational constant.
• Its value in SI unit is 6.674 × 10^–11 Nm2 kg^–2.

Acceleration due to gravity (g):

• When you throw any object upwards, its velocity ceases at a particular height and then it falls down due to the gravitational force of the Earth.
• The velocity of the object keeps changing as it falls down.
• This change in velocity must be due to the force acting on the object.
• The acceleration of the body is due to the Earth’s gravitational force.
• So, it is called as ‘acceleration due to the gravitational force of the Earth’ or ‘acceleration due to gravity of the Earth’.
• It is represented as ‘g’. Its unit is ms^–2
• Mean value of the acceleration due to gravity is taken as 9.8 m s^–2 on the surface of the Earth.
• This means that the velocity of a body during the downward free fall motion varies by 9.8 ms^–1 for every 1 second.
• However, the value of ‘g’ is not the same at all points on the surface of the earth.

Application of Newton’s law of gravitation:

• Dimensions of the heavenly bodies can be measured using the gravitation law. Mass of the Earth, radius of the Earth, acceleration due to gravity, etc. can be calculated with a higher accuracy.
• Helps in discovering new stars and planets.
• One of the irregularities in the motion of stars is called ‘Wobble’ lead to the disturbance in the motion of a planet nearby. In this condition the mass of the star can be calculated using the law of gravitation.
• Helps to explain germination of roots is due to the property of geotropism which is the property of a root responding to the gravity.
• Helps to predict the path of the astronomical bodies.

The Relationship between g and G:

• When a body is at rests on the surface of the Earth, it is acted upon by the gravitational force of the Earth.
• Let us compute the magnitude of this force in two ways.
• Let, M be the mass of the Earth and m be the mass of the body.
• The entire mass of the Earth is assumed to be concentrated at its centre.
• The radius of the Earth is R =6378 km (= 6400 km approximately).
• By Newton’s law of gravitation, the force acting on the body is given by
  
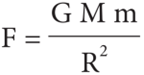
• Here, the radius of the body considered is negligible when compared with the Earth’s radius.
• Now, the same force can be obtained from Newton’s second law of motion.
• According to this law, the force acting on the body is given by the product of its mass and acceleration (called as weight).
• Here, acceleration of the body is under the action of gravity hence a = g

F = ma = mg

F = weight = mg

Comparing equations,

Acceleration due to gravity

Mass of the Earth (M)

The mass of the Earth is obtained as follows:

• Mass of the Earth M = g R² /G
• Substituting the known values of g, R and G, you can calculate the mass of the Earth as

M = 5.972 × 10²⁴ kg

Variation of acceleration due to gravity (g):

• Since, g depends on the geometric radius of the Earth, (g ∝ 1/R²), its value changes from one place to another on the surface of the Earth.
• Since, the geometric radius of the Earth is maximum in the equatorial region and minimum in the polar region, the value of g is maximum in the polar region and minimum at the equatorial region.
• When you move to a higher altitude from the surface of the Earth, the value of g reduces.
• In the same way, when you move deep below the surface of the Earth, the value of g reduces. (This topic will be discussed in detail in the higher classes).
• Value of g is zero at the centre of the Earth.

Mass and Weight:

• Mass:
• Mass is the basic property of a body. Mass of a body is defined as the quantity of matter contained in the body.
• Its SI unit is kilogram (kg).
• Weight:
• Weight of a body is defined as the gravitational force exerted on a body due to the gravity.

Weight = Gravitational Force

= mass (m) × acceleration due to gravity (g).

g = acceleration due to gravity for Earth (at sea level) = 9.8 ms^–2.

• Weight is a vector quantity.
• Direction of weight is always towards the centre of the Earth.
• SI unit of weight is newton (N).
• Weight of a body varies from one place to another place on the Earth since it depends on the acceleration due to gravity of the Earth (g) weight of a body is more at the poles than at the equatorial region.
• The value of acceleration due to gravity on the surface of the moon is 1.625 ms^-2.
• This is about 0.1654 times the acceleration due to gravity of the Earth.
• If a person whose mass is 60 kg stands on the surface of Earth, his weight would be 588 N (W = mg = 60 × 9.8).
• If the same person goes to the surface of the Moon, he would weigh only 97.5 N (W = 60 × 1.625).
• But, his mass remains the same (60 kg) on both the Earth and the Moon.

The Astronaut’s Weight Loss:

• Some of us believe that the astronauts in the orbiting space station do not experience any gravitational force of the Earth. So they float.
• But this is absolutely wrong.
• Astronauts are not floating but falling freely around the earth due to their huge orbital velocity.
• Since space station and astronauts have equal acceleration, they are under free fall condition.
• Hence, both the astronauts and the space station are in the state of weightlessness.

The Same Speed Both Day and Night with Respect to Sun:

• Earth orbits the Sun in an elliptical orbit.
• Let us specify the velocity of the centre of Earth with respect to Sun as .
• This is due to the elliptical motion of the Earth around the Sun.
• We know that at the same time Earth is also spinning on its own axis.
• Due to this spinning, all objects on the surface of the Earth undergo circular motion with velocity () with respect to the axis of rotation of the Earth.
• At night both and  are either in the same direction or at an acute angle with each other.
• So, the velocity of an object on the surface of Earth with respect to Sun at night time is .
• During the day and  are either in opposite directions or at an obtuse angle with each other.
• So, the velocity of the object with respect to Sun at day time .
• From this, we can conclude that any object on the surface of the Earth travels faster with respect to Sun during night than during day time.
• This happens due to the rotation of the Earth.

Centripetal force:

• If a particle is in uniform circular motion, there must be centripetal acceleration towards the centre of the circle.
• If there is acceleration then there must be some force acting on it with respect to an inertial frame.
• This force is called centripetal force.

Examples:

• In the case of whirling motion of a stone tied to a string, the centripetal force on the particle is provided by the tensional force on the string.
• In circular motion in an amusement park, the centripetal force is provided by the tension in the iron ropes.
• In motion of satellites around the Earth, the centripetal force is given by Earth’s gravitational force on the satellites.
• Newton’s second law for satellite motion is

Where r- distance of the planet from the centre of the Earth.

m – Mass of the satellite

v – Speed of the satellite

• When a car is moving on a circular track the centripetal force is given by the frictional force between the road and the tyres.
• Newton’s second law for this case is
• Even when the car moves on a curved track, the car experiences the centripetal force which is provided by frictional force between the surface and the tyre of the car.
• When the planets orbit around the Sun, they experience centripetal force towards the centre of the Sun.
• Here gravitational force of the Sun acts as centripetal force on the planets

Centrifugal Force:

• Consider the case of a whirling motion of a stone tied to a string.
• Assume that the stone has angular velocity ω in the inertial frame (at rest).
• If the motion of the stone is observed from a frame which is also rotating along with the stone with same angular velocity ω then, the stone appears to be at rest.
• This implies that in addition to the inward centripetal force ­-mω² r there must be an equal and opposite force that acts on the stone outward with value +mω²
• So the total force acting on the stone in a rotating frame is equal to zero (­ -mω² r + mω² r = 0).
• This outward force +mω² r is called the centrifugal force.

Effects of Centrifugal Force:

• Although centrifugal force is a pseudo force, its effects are real.
• When a car takes a turn in a curved road, person inside the car feels an outward force which pushes the person away.
• This outward force is also called centrifugal force.
• If there is sufficient friction between the person and the seat, it will prevent the person from moving outwards.
• When a car moving in a straight line suddenly takes a turn, the objects not fixed to the car try to continue in linear motion due to their inertia of direction.
• While observing this motion from an inertial frame, it appears as a straight line.
• But, when it is observed from the rotating frame it appears to move outwards.
• A person standing on a rotating platform feels an outward centrifugal force and is likely to be pushed away from the platform.
• Many a time the frictional force between the platform and the person is not sufficient to overcome outward push.
• To avoid this, usually the outer edge of the platform is little inclined upwards which exerts a normal force on the person which prevents the person from falling.

The Motion of a Vehicle Moving on an Even Circular Road:

• When a vehicle travels in a curved path, there must be centripetal force acting on it.
• This centripetal force is provided by the frictional force between tyre and surface of the road. Consider a vehicle of mass ‘m’ moving at a speed ‘v’ in the circular track of radius ‘r’.
• There are three forces acting on the vehicle when it moves.
• Gravitational force (mg) acting downwards
• Normal force (N) acting upwards
• Frictional force (F_S) acting horizontally inwards along the road
• Suppose the road is horizontal then the normal force and gravitational force are exactly equal and opposite.
• The centripetal force is provided by the force of static friction Fs between the tyre and surface of the road which acts towards the centre of the circular track,
• As we have already seen in the previous section, the static friction can increase from zero to a maximum value
• There are two conditions possible:
• The static friction would be able to provide necessary centripetal force to bend the car on the road.
• So the coefficient of static friction between the tyre and the surface of the road determines what maximum speed the car can have for safe turn.
• If the static friction is not able to provide enough centripetal force to turn, the vehicle will start to skid.

The Cause of Raising the Outer Edge of the Road:

• In a leveled circular road, skidding mainly depends on the coefficient of static friction the coefficient of static friction depends on the nature of the surface which has a maximum limiting value.
• To avoid this problem, usually the outer edge of the road is slightly raised compared to inner edge.
• This is called banking of roads or tracks.
• This introduces an inclination, and the angle is called banking angle.
• Let the surface of the road make angle θ with horizontal surface.
• Then the normal force makes the same angle θ with the vertical.
• When the car takes a turn, there are two forces acting on the car:
• Gravitational force mg (downwards)
• Normal force N (perpendicular to surface)
• We can resolve the normal force into two components.

N cosθ and N sinθ.

• The component N cosθ balances the downward gravitational force ‘mg’ and component N sinθ will provide the necessary centripetal acceleration.
• By using Newton second law
• The banking angle θ and radius of curvature of the road or track determines the safe speed of the car at the turning.
• If the speed of car exceeds this safe speed, then it starts to skid outward but frictional force comes into effect and provides an additional centripetal force to prevent the outward skidding.
• At the same time, if the speed of the car is little lesser than safe speed, it starts to skid inward and frictional force comes into effect, which reduces centripetal force to prevent inward skidding.
• However, if the speed of the vehicle is sufficiently greater than the correct speed, then frictional force cannot stop the car from skidding.