2. MECHANICS AND PROPERTIES OF MATTER – TNPSC 1 MNT Free IAS Coaching

2.MECHANICS-AND-PROPERTIES-OF-MATTER

3.Mechanics and Properties of Matter

Rubber or steel:

Steel is more elastic than rubber.
If an equal stress is applied to both steel and rubber, the steel produces less strain.
So the Young’s modulus is higher for steel than rubber.
The object which has higher Young’s modulus is more elastic.

Terminal Velocity:

To understand terminal velocity, consider a small metallic sphere falling freely from rest through a large column of a viscous fluid.
The forces acting on the sphere are
Gravitational force of the sphere acting vertically downwards,
Up thrust U due to buoyancy and
Viscous drag acting upwards (viscous force always acts in a direction opposite to the motion of the sphere).
Initially, the sphere is accelerated in the downward direction so that the upward force is less than the downward force.
As the velocity of the sphere increases, the velocity of the viscous force also increases.
A stage is reached when the net downward force balances the upward force and hence the resultant force on the sphere becomes zero.
It now moves down with a constant velocity.
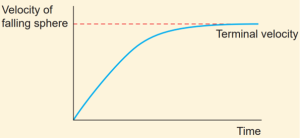
The maximum constant velocity acquired by a body while falling freely through a viscous medium is called the terminal velocity v_t.
A graph is drawn with velocity along y- axis and time along x- axis.
It is evident from the graph that the sphere is accelerated initially and in course of time it becomes constant, and attains terminal velocity (v_t).

Expression for terminal velocity:

Consider a sphere of radius r which falls freely through a highly viscous liquid of coefficient of viscosity η.
Let the density of the material of the sphere be ρ and the density of the fluid be σ.
Gravitational force acting on the sphere,
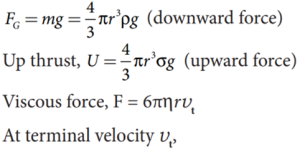
The net downward force = upward force
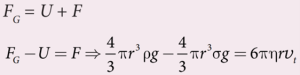
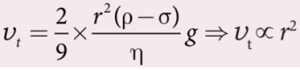
Here, it should be noted that the terminal speed of the sphere is directly proportional to the square of its radius.
If σ is greater than ρ, then the term (ρ – σ) becomes negative leading to a negative terminal velocity.
That is why air bubbles rise up through water or any fluid.
This is also the reason for the clouds in the sky to move in the upward direction.

Stoke’s Law and Its Applications:

When a body falls through a viscous medium, it drags the layer of the fluid immediately in contact with it.
This produces a relative motion between the different layers of the liquid.
Stoke performed many experiments on the motion of small spherical bodies in different fluids and concluded that the viscous force F acting on a spherical body of radius r depends directly on

Radius (r) of the sphere

Velocity (v) of the sphere and

Coefficient of viscosity η of the liquid

Therefore F ∝ η^xr^yv^z^⇒ F = k η^xr^yv^z, where k is a dimensionless constant.
Using dimensions, the above equation can be written as
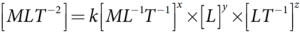
On solving, we get x=1, y=1, and z=1
Therefore, F=kη rv
Experimentally, Stoke found that the value of k = 6π
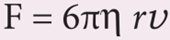
This relation is known as Stoke’s law

Practical applications of Stoke’s law:

Since the raindrops are smaller in size and their terminal velocities are small, remain suspended in air in the form of clouds.
As they grow up in size, their terminal velocities increase and they start falling in the form of rain.
This law explains the following:
Floatation of clouds
Larger raindrops hurt us more than the smaller ones
A man coming down with the help of a parachute acquires constant terminal velocity.

Viscosity & Its Applications:

When a liquid is flowing, there is a frictional force between the successive layers of the liquid.
This force which acts in order to oppose the relative motion of the layer is known as viscous force.
Such a property of a liquid is called viscosity.
Viscosity force is measured by the unit called poise in CGS and kg m^–1 s^–1 or N s m^–2 in SI.

Applications of viscosity:

The importance of viscosity can be understood from the following examples.
The oil used as a lubricant for heavy machinery parts should have a high viscous coefficient.
To select a suitable lubricant, we should know its viscosity and how it varies with temperature [Note: As temperature increases, the viscosity of the liquid decreases].
Also, it helps to choose oils with low viscosity used in car engines (light machinery).
The highly viscous liquid is used to damp the motion of some instruments and is used as brake oil in hydraulic brakes.
Blood circulation through arteries and veins depends upon the viscosity of fluids.
Millikan conducted the oil drop experiment to determine the charge of an electron.
He used the knowledge of viscosity to determine the charge.

Intermolecular forces:

Some liquids do not mix together due to their physical properties such as density, surface tension force, etc.
For example, water and kerosene do not mix together.
Mercury does not wet the glass but water sticks to it.
Water rises up to the leaves through the stem.
They are mostly related to the free surfaces of liquids.
Liquids have no definite shape but have a definite volume.
Hence they acquire a free surface when poured into a container.
Therefore, the surfaces have some additional energy, called as surface energy.
The phenomenon behind the above fact is called surface tension.
Laplace and Gauss developed the theory of surface and motion of a liquid under various situations.
The molecules of a liquid are not rigidly fixed like in a solid.
They are free to move about.
The force between the like molecules which holds the liquid together is called ‘cohesive force’.
When the liquid is in contact with a solid, the molecules of these solid and liquid will experience an attractive force which is called ‘adhesive force’.
These molecular forces are effective only when the distance between the molecules is very small about 10^–9 m (i.e., 10 Å).
The distance through which the influence of these molecular forces can be felt in all directions constitute a range and is called sphere of influence.
The forces outside this range are rather negligible.
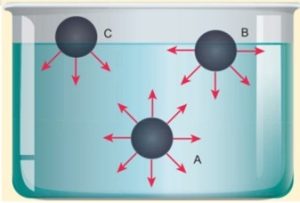
Consider three different molecules A, B, and C in a given liquid.
Let a molecule ‘A’ be considered well inside the liquid within the sphere of influence.
Since this molecule interacts with all other molecules in all directions, the net force experienced by A is zero.
Now consider a molecule ‘B’ in which three-fourth lies below the liquid surface and one–fourth on the air.
Since B has more molecules towards its lower side than the upper side, it experiences a net force in the downward direction.
In a similar way, if another molecule ‘C’ is chosen on the liquid surface (i.e, upper half in air and lower half in liquid), it experiences a maximum downward force due to the availability of more number of liquid molecules on the lower part.
Hence it is obvious that all molecules of the liquid that falls within the molecular range inside the liquid interact with the molecule and hence experience a downward force.
When any molecule is brought towards the surface from the interior of the liquid, work is done against the cohesive force among the molecules of the surface.
This work is stored as potential energy in molecules.
So the molecules on the surface will have greater potential energy than that of molecules in the interior of the liquid.
But for a system to be under stable equilibrium, its potential energy (or surface energy) must be a minimum.
Therefore, in order to maintain stable equilibrium, a liquid always tends to have a minimum number of molecules.
In other words, the liquid tends to occupy a minimum surface area.
This behavior of the liquid gives rise to surface tension.

Surface Tension:

Water bugs and water striders walk on the surface of water.
The water molecules are pulled inwards and the surface of water acts like a springy or stretched membrane.
This balance the weight of water bugs and enables them to walk on the surface of water.
We call this phenomenon as surface tension.
The hairs of the painting brush cling together when taken out of water.
This is because the water films formed on them tends to contract to a minimum area.

Factors affecting the surface tension of a liquid:

The presence of any contamination or impurities considerably affects the force of surface tension depending upon the degree of contamination.
The presence of dissolved substances can also affect the value of surface tension.
For example, a highly soluble substance like sodium chloride (NaCl) when dissolved in water (H2 0) increases the surface tension of water.
But the sparingly soluble substance like phenol or soap solution when mixed in water decreases the surface tension of water.
Electrification affects the surface tension.
When a liquid is electrified, surface tension decreases.
Since external force acts on the liquid surface due to electrification, area of the liquid surface increases which acts against the contraction phenomenon of the surface tension. Hence, it decreases.
Temperature plays a very crucial role in altering the surface tension of a liquid.
Obviously, the surface tension decreases linearly with the rise of temperature.
For a small range of temperature, the surface tension at T_t at t^oC is T_t = T₀ (1− α t)
Where, T₀ is the surface tension at temperature 0^oC and α is the temperature coefficient of surface tension.
It is to be noted that at the critical temperature, the surface tension is zero as the interface between liquid and vapour disappear.
For example, the critical temperature of water is 374^o Therefore, the surface tension of water is zero at that temperature.
van der Wall suggested the important relation between the surface tension and the critical temperature as
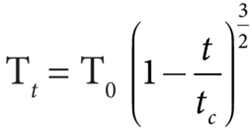
Generalizing the above relation, we get
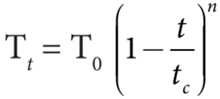
Which gives more accurate value.
Here, n varies for different liquids and t and t_c denote the temperature and critical temperature in absolute scale (Kelvin scale) respectively.

Surface Tension:

All the above questions have an answer, i.e., “due to surface tension”.
Surface tension is the property of a liquid.
The molecules of a liquid experience a force, which contracts the extent of their surface area as much as possible, so as to have the minimum value.
Thus, the amount of force acting per unit length, on the surface of a liquid is called surface tension.
It has the unit N m^–1.

The excess pressure inside a liquid droplet, soap bubble and air bubble:

As it is discussed earlier, the free surface of a liquid becomes curved when it has contact with a solid.
Depending upon the nature of liquid-air or liquid-gas interface, the magnitude of interfacial surface tension varies.
In other words, as a consequence of surface tension, the above such interfaces have energy and for a given volume, the surface will have a minimum energy with least area.
Due to this reason, the liquid drop becomes spherical (for a smaller radius).
When the free surface of the liquid is curved, there is a difference in pressure between the inner and outer the side of the surface.
When the liquid surface is plane, the forces due to surface tension (T, T) act tangentially to the liquid surface in opposite directions.
Hence, the resultant force on the molecule is zero.
Therefore, in the case of a plane liquid surface, the pressure on the liquid side is equal to the pressure on the vapour side.
When the liquid surface is curved, every molecule on the liquid surface experiences forces (F_T, F_T) due to surface tension along the tangent to the surface.
Resolving these forces into rectangular components, we find that horizontal components cancel out each other while vertical components get added up.
Therefore, the resultant force normal to the surface acts on the curved surface of the liquid.
Similarly, for a convex surface, the resultant force is directed inwards towards the centre of curvature, whereas the resultant force is directed outwards from the centre of curvature for a concave surface.
Thus, for a curved liquid surface in equilibrium, the pressure on its concave side is greater than the pressure on its convex side.

Excess of pressure inside a bubble and a liquid drop:

The small bubbles and liquid drops are spherical because of the forces of surface tension.
The fact that a bubble or a liquid drop does not collapse due to the combined effect indicates that the pressure inside a bubble or a drop is greater than that outside it.

Excess of pressure inside air bubble in a liquid:

Consider an air bubble of radius R inside a liquid having surface tension T.
Let P₁ and P₂ be the pressures outside and inside the air bubble, respectively.
Now, the excess pressure inside the air bubble is ΔP = P₁ − P₂.
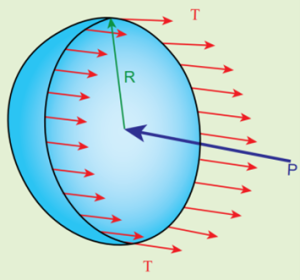
In order to find the excess pressure inside the air bubble, let us consider the forces acting on the air bubble.
For the hemispherical portion of the bubble, considering the forces acting on it, we get,
The force due to surface tension acting towards right around the rim of length 2πR is F_T = 2πRT
The force due to outside pressure P₁ is to the right acting across a cross sectional area of πR² is F_P1 = P₁ πR²
The force due to pressure P₂ inside the bubble, acting to the left is F_P2 = P₂ πR².
As the air bubble is in equilibrium under the action of these forces, F_P2 = F_T + F_P1

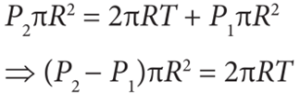
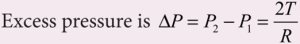
Excess pressure inside a soap bubble:

Consider a soap bubble of radius R and the surface tension of the soap bubble be T.
A soap bubble has two liquid surfaces in contact with air, one inside the bubble and other outside the bubble.
Therefore, the force on the soap bubble due to surface tension is 2×2πRT.
The various forces acting on the soap bubble are
Force due to surface tension F_T= 4πRT towards right
Force due to outside pressure, F_P1 = P₁ πR² towards right
Force due to inside pressure, F_P2 = P₂ πR² towards left
As the bubble is in equilibrium, F_P2 = F_T + F_P1

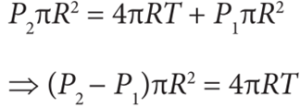
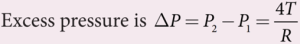
Excess pressure inside the liquid drop:

Consider a liquid drop of radius R and the surface tension of the liquid is T.
The various forces acting on the liquid drop are,
Force due to surface tension F_T=2πRT towards right
Force due to outside pressure, F_P1 = P₁ πR² towards right
Force due to inside pressure, F_P2 = P₂ πR² towards left
As the drop is in equilibrium, F_P2 = F_T + F_P1

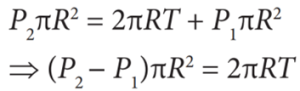
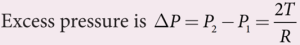
Capillarity:

The word ‘capilla’ means hair in Latin.
If the tubes were hair thin, then the rise would be very large.
It means that the tube having a very small diameter is called a ‘capillary tube’.
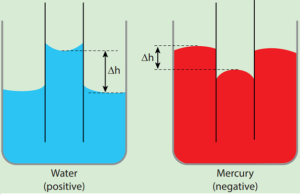
When a glass capillary tube open at both ends is dipped vertically in water, the water in the tube will rise above the level of water in the vessel.
In case of mercury, the liquid is depressed in the tube below the level of mercury in the vessel.
In a liquid whose angle of contact with solid is less than 90°, suffers capillary rise.
On the other hand, in a liquid whose angle of contact is greater than 90°, suffers capillary fall.
The rise or fall of a liquid in a narrow tube is called capillarity or capillary action.
Depending on the diameter of the capillary tube, liquid rises or falls to different heights.

Practical applications of capillarity:

Due to capillary action, oil rises in the cotton within an earthen lamp.
Likewise, sap rises from the roots of a plant to its leaves and branches.
Absorption of ink by a blotting paper
Capillary action is also essential for the tear fluid from the eye to drain constantly.
Cotton dresses are preferred in summer because cotton dresses have fine pores which act as capillaries for sweat.

Berneli’s Theorem & its applications:

According to Bernoulli’s theorem, the sum of pressure energy, kinetic energy, and potential energy per unit mass of an incompressible, non-viscous fluid in a streamlined flow remains a constant. Mathematically,
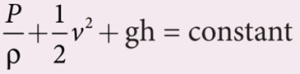
This is known as Bernoulli’s equation.

Applications of Bernoulli’s Theorem:

Blowing off roofs during wind storm:

In olden days, the roofs of the huts or houses were designed with a slope.
One important scientific reason is that as per the Bernoulli’s principle, it will be safeguarded except roof during storm or cyclone.
During cyclonic condition, the roof is blown off without damaging the other parts of the house.
In accordance with the Bernoulli’s principle, the high wind blowing over the roof creates a low-pressure P₁.
The pressure under the roof P₂ is greater.
Therefore, this pressure difference (P₂ –P₁) creates an up thrust and the roof is blown off.

Aerofoil lift:

The wings of an airplane (aerofoil) are so designed that its upper surface is more curved than the lower surface and the front edge is broader than the real edge.
As the aircraft moves, the air moves faster above the aerofoil than at the bottom.
According to Bernoulli’s Principle, the pressure of air below is greater than above, which creates an up thrust called the dynamic lift to the aircraft.

Bunsen burner:

In this, the gas comes out of the nozzle with high velocity, hence the pressure in the stem decreases.
So outside air reaches into the burner through an air vent and the mixture of air and gas gives a blue flame.

Venturimeter:

This device is used to measure the rate of flow (or say flow speed) of the incompressible fluid flowing through a pipe.
It works on the principle of Bernoulli’s theorem.
It consists of two wider tubes A and A’ (with cross sectional area A) connected by a narrow tube B (with cross sectional area a).
A manometer in the form of U-tube is also attached between the wide and narrow tubes.
The manometer contains a liquid of density ‘ρ_m’.
Let P₁ be the pressure of the fluid at the wider region of the tube A.
Let us assume that the fluid of density ‘ρ’ flows from the pipe with speed ‘v₁’ and into the narrow region, its speed increases to ‘v₂’.
According to the Bernoulli’s equation, this increase in speed is accompanied by a decrease in the fluid pressure P₂ at the narrow region of the tube B.
Therefore, the pressure difference between the tubes A and B is noted by measuring the height difference (ΔP = P₁ −P₂) between the surfaces of the manometer liquid.
From the equation of continuity, we can say that Av₁ = a v₂ which means that
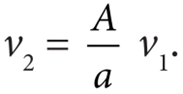
Using Bernoulli’s equation,
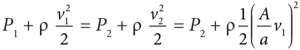
From the above equation, the pressure difference
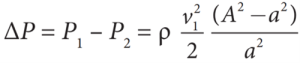
Thus, the speed of flow of fluid at the wide end of the tube A
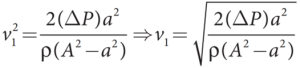
The volume of the liquid fl owing out per second is

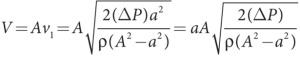
Other applications:

This Bernoulli’s concept is mainly used in the design of carburetor of automobiles, filter pumps, atomizers, and sprayers.
For example, the carburetor has a very fine channel called nozzle through which the air is allowed to flow in larger speed.
In this case, the pressure is lowered at the narrow neck and in turn, the required fuel or petrol is sucked into the chamber so as to provide the correct mixture of air and fuel necessary for ignition process.

Spider Webs:

A spider web is much stronger than what we think.
A single strand of spider silk can stop flying insects which are tens and thousands times its mass.
The young’s modulus of the spider web is approximately 4.5 × 10⁹ N m⁻².