இயக்கச் சமன்பாடுகள்:

முதல் இயக்கச் சமன்பாடு:

வரையறைப்படி முடுக்கம் (a)

= திசைவேக மாறுபாடு / காலம்

= (இறுதித் திசைவேகம் – தொடக்கத் திசைவேகம்) / காலம்

at = (OC – OD) / OE = DC / OE = DC / t

DC = at = AB

வரைபடத்திலிருந்து, EB = EA + AB

v=u + at

இது முதல் இயக்கச் சமன்பாடு ஆகும்.

இரண்டாம் இயக்கச் சமன்பாடு:

வரைபடத்திலிருந்து, ‘t’ காலத்தில் பொருள் ஒன்று கடந்த தொலைவான நாற்கரத்தின் பரப்பளவு DOEB மூலம் கொடுக்கப்படுகிறது.

S = நாற்கரத்தின் பரப்பளவு DOEB

= செவ்வகத்தின் பரப்பளவு DOEA + முக்கோணத்தின் பரப்பளவு DAB

= (AEX OE) + 1/2 x (AB x DA)

S = ut + 1/2 at²

இது இரண்டாம் இயக்கச் சமன்பாடு ஆகும்.

மூன்றாவது இயக்கச் சமன்பாடு

‘t’, காலத்தில் பொருள் கடந்த தொலைவை வரைபடத்தில் நாற்கரம் DOEB யின் பரப்பளவானது குறிக்கிறது. இங்கு DOEB என்பது சரிவகத்தையும் குறிக்கிறது.

 S = சரிவகம் DOEB யின் பரப்பளவு

= 1/2 x இணைப் பக்க நீளங்களின் கூடுதல் x இணைப் பக்கங்களுக்கு இடைப்பட்ட தொலைவு

= 1/2 x (OD + BE) x OE

S = 1/2 x (u + v) x t

ஆனால், முடுக்கம் a = (v – u) / t அல்லது

t = (v – u)/a

எனவே, s = 1/2 x (v + u) x (v – u)/a

2as = v² – u²

v² = u² + 2as

இது மூன்றாம் இயக்கச் சமன்பாடு ஆகும்.

தடையின்றி தானே விழும் பொருளின் பொருளின் இயக்கம்:

கல் மற்றும் அழிப்பான் இரண்டும் பூமியின் மேல்பரப்பை சற்றேறக்குறைய ஒரே நேரத்தில் வந்தடைந்தன என்பதைக் காண முடியும். ஆனால், அழிப்பானையும், காகிதத்தையும் கீழே விடும் பொழுது அழிப்பான் முதலில் வந்தடைகிறது. காகிதத்தாள் பின்னர் வந்தடைகிறது. அதைப்போலவே காகிதத்தாளும், பந்துபோல் சுருட்டப்பட்ட காகிதமும் ஒரே எடையைப் பெற்றிருந்த போதும், பந்து போல் சுருட்டப்பட்ட காகிதம் முதலாவதும், காகிதத் தாள் இரண்டாவதும் தரையை வந்தடைவதைக் காணலாம். இதற்கான காரணம் உங்களுக்குத் தெரியுமா? காற்றில்லாத வெற்றிடத்தில் மேற்சொன்ன அனைத்துப் பொருட்களும் ஒரே நேரத்தில் தரையை வந்தடையும். காற்று ஊடகத்தில் காற்றின் உராய்வு விசையானது தடையின்றி தானே விழும் பொருளின் மீது ஒரு தடையை ஏற்படுத்துகிறது.

அழிப்பான் மற்றும் கல்லின் மீது செயல்படும் இந்த காற்றுத்தடை புவிஈர்ப்பு விசையுடன் ஒப்பிடும்போது புறக்கணிக்கத் தக்கதாகும். எனவே அவையிரண்டும் ஏறத்தாழ ஒரே நேரத்தில் தரையை வந்தடைகின்றன. இந்த செயல்பாடுகளின் மூலம், காற்றுத் தடையின் அளவானது, பொருளின் பரப்பளவைப் பொறுத்துள்ளது என்பதை அறியலாம்.

தடையின்றி கீழே விழும் பொருட்கள் முடுக்கமடையும் என்பது நமக்குத் தெரிந்ததே. இந்த முடுக்கம் பொருளின் நிறையைப் பொருத்தது அல்ல. அதாவது, உள்ளீடற்ற பொருள் அல்லது திடப்பொருள் மற்றும் சிறிய அல்லது பெரிய பொருட்கள் அனைத்தும் ஒரே கால வீதத்தில் கீழே விழும். முடுக்கம் a க்குப் பதிலாக புவிஈர்ப்பு முடுக்கம் ‘g’ ஐப் பிரதியிடுவதால், தடையின்றி தானே கீழே விழும் பொருட்களுக்கான சமன்பாடுகளைப் பெற முடியும். தடையின்றி தானே விழும் பொருட்களுக்கு அதன் ஆரம்பத் திசைவேகம் u = 0. எனவே, கீழ்க்காணும் சமன்பாடுகளைப் பெற முடியும்.

v = gt, s = 1/2 gt², v² = 2gh

ஒரு பொருளை மேல்நோக்கி எறியும் பொழுது அது, புவியீர்ப்பு விசைக்கு எதிர்த்திசையில் செல்கிறது. எனவே, ‘a’ க்கு பதிலாக -g என்றும் எடுத்துக்கொள்ள வேண்டும். கீழ்நோக்கிச் செல்லும்போது, +g என எடுத்துக்கொள்ள வேண்டும்.

நியூட்டனின் இயக்க விதிகள்:

நியூட்டனின் முதல் விதி:

ஒவ்வொரு பொருளும் புறவிசை ஏதும் செயல்படாத வரையில், தமது ஓய்வு நிலையிலோ அல்லது சீராக இயங்கிக் கொண்டிருக்கும் நேர்க்கோட்டு நிலையிலோ தொடர்ந்து இருக்கும். இவ்விதி விசையினை வரையறுக்கிறது. அது மட்டுமின்றி, பொருட்களின் நிலைமத்தையும் விளக்குகிறது.

நியூட்டனின் இரண்டாம் இயக்க விதி:

பொருள் ஒன்றின் மீது செயல்படும் விசையானது அப்பொருளின் உந்தமாறுபாட்டு வீதத்திற்கு நேர்தகவில் அமையும். மேலும் இந்த உந்த மாறுபாடு விசையின் திசையிலேயே அமையும். இவ்விதி விசையின் எண்மதிப்பை அளவிட உதவுகிறது. எனவே இதை ‘விசையின் விதி’ என்றும் அழைக்கலாம்.

விசைக்கான சமன்பாட்டை கீழ்க்கண்டவாறு தருவிக்கலாம்.

m நிறை மதிப்புடைய பொருள் ஒன்று u என்ற ஆரம்ப திசைவேகத்தில் நேர்க்கோட்டு இயக்கத்தில் உள்ளதென கொள்வோம். t என்ற கால இடைவெளியில் F என்ற சமன் செயப்படாத புற விசையின் தாக்கத்தால், அதன் வேகம் v என்று மாற்றமடைகிறது.

பொருளின் ஆரம்ப உந்தம் P_i = mu

இறுதி உந்தம் P_f = mv

உந்தமாறுபாடு Δp = Pf – Pi = mv – m u நியூட்டனின் இரண்டாம் இயக்க விதிப்படி விசை F α உந்த மாற்றம்/ காலம்

F α (mv – mu) /t

F = K m (v- u)/t

K என்பது விகித மாறிலி; K=1 (அனைத்து அலகு முறைகளிலும்) எனவே

F= (mv – mu) /t

முடுக்கம் = திசை வேகமாற்றம்/ காலம்;

a = (v – u)/t எனவே

F=m x a

விசை = நிறை x முடுக்கம்

சீரான திசைவேகத்தில் நகரும் பொருளினை, தொடர்ந்து நகர்த்த புறவிசை ஏதும் தேவையில்லை. புறவிசைகளின் தொகுபயன் மதிப்பு சுழியாக இல்லை எனில் திசைவேக மதிப்பில் உறுதியாக மாற்றம் இருக்கும். உந்த மாற்றமானது விசையின் திசையிலேயே அமையும். இம்மாற்றமானது அதன் எண் மதிப்பிலோ, திசையிலோ அல்லது இவை இரண்டிலுமோ ஏற்படலாம்.

விசை முடுக்கத்தினை ஏற்படுத்துகிறது. சீரான வட்ட இயக்கத்தில் உள்ள பொருளின் திசைவேகத்தின் எண்மதிப்பு மாறிலியாகும். இருப்பினும் பொருளானது வட்டப்பாதையின் ஒவ்வோர் புள்ளியிலும் தனது திசையினை தொடர்ந்து மாற்றி கொள்வதால், திசைவேக மாறுபாடு ஏற்படுகிறது. இது முடுக்கத்தினை சுழற்சி ஆரத்தில் ஏற்படுத்துகிறது.

இம்முடுக்கம் மைய விலக்கு முடுக்கம் எனப்படும். இம் முடுக்கம் உருவாக காரணமான விசை மைய விலக்கு விசை என்றழைக்கப்படுகிறது. இதைப்பற்றி ஒன்பதாம் வகுப்பில் நீங்கள் கற்றறிந்திருப்பீர்கள்.

விசையின் அலகு: விசையின் SI அலகு நியூட்டன் (N) ஆகும். அதன் CGS அலகு டைன் (dyne) ஆகும்.

1 நியூட்டன் என்பதன் வரையறை: 1 கிலோகிராம் நிறையுடைய பொருளொன்றை 1 மீவி^-2 அளவிற்கு முடுக்குவிக்க தேவைப்படும் விசையின் அளவு 1 நியூட்டன் (1N) ஆகும். 1 நியூட்டன் = 1கிகி மீவி^-2

1 டைன் என்பதன் வரையறை: 1 கிராம் நிறையுடைய பொருளொன்றை 1 செமீவி^-2 அளவிற்கு முடுக்குவிக்க தேவைப்படும் விசையின் அளவு 1 டைன் ஆகும். 1 டைன் = 1 கிசெமீவி^-2.

1 நியூட்டன் = 10⁵ டைன்

ஓரலகு விசை

1 கிலோகிராம் நிறையுள்ள பொருளொன்றை 1 மீவி^-2 அளவிற்கு முடுக்கவிக்க தேவைப்படும் விசையின் அளவு ஒரு நியூட்டன் (1 N) ஆகும். இது ஓரலகு விசை என்றழைக்கப்படுகிறது.

ஈர்ப்பியல் அலகு விசை (Gravitational unit of force):

ஓரலகு நிறையுள்ள (1 கி கி) பொருளொன்றை புவியின் ஈர்ப்பு முடுக்கதிற்கு (9.8 மீ வி^-2) இணையாக முடுக்கவிக்க தேவைப்படும் விசையின் அளவு ஈர்ப்பியல் அலகுவிசை எனப்படும்.

ஈர்ப்பியல் அலகுவிசையின் SI அலகு, கிலோகிராம் விசை (kgf) ஆகும். CGS அலகு முறையில் கிராம் விசை (gf) ஆகும்

1 kg f =1 kg x 9.8 ms^-2 = 9.8 நியூட்ட ன்;

1gf =1g x 980 cms^-2 = 980 டைன்

நியூட்டனின் மூன்றாம் இயக்க விதி

ஒவ்வொரு விசைக்கும் சமமான எதிர் விசை உண்டு. விசையும் எதிர்விசையும் எப்போதும் இரு வேறு பொருள்கள் மீது செயல்படும்.

A என்ற பொருள் ஒன்று B என்ற பொருளின் மீது F_A விசையினை செலுத்துகிறது எனில், ‘B’ ஆனது தன் எதிர்விசை F_B யினை A மீது செலுத்தும். இவற்றின் எண்மதிப்பு சமம். ஆனால் அவை ஒன்றுக்கொன்று எதிர்திசையில் செயல்படும்.

F_A = – F_B

சில எடுத்துக்காட்டுகள்

• பறவைகள் தமது சிறகுகளின் விசை(விசை) மூலம் காற்றினை கீழே தள்ளுகின்றன. காற்றானது அவ்விசைக்கு சமமான விசையினை (எதிர் விசை) உருவாக்கி பறவையை மேலே பறக்க வைக்கிறது.
• நீச்சல் வீரர் ஒருவர் நீரினை கையால் பின்நோக்கி தள்ளுதலின் மூலம் விசையினை ஏற்படுத்துகிறார். நீரானது அந்நபரை விசைக்கு சமமான எதிர்விசை கொண்டு முன்னே தள்ளுகிறது.

துப்பாக்கி சுடுதலில் குண்டு, விசையுடன் முன்னோக்கி செல்ல அதற்கு சமமான எதிர்விசையினால் குண்டு வெடித்தபின் துப்பாக்கி பின்னோக்கி நகர்கிறது.

கணத்தாக்கு விசை:

மிகக் குறைந்த காலஅளவில் மிக அதிக அளவு செயல்படும் விசை, கணத்தாக்கு விசை எனப்படும்.

F என்ற விசை t காலஅளவில் ஒரு பொருள் மீது செயல்பட்டால், ஏற்படும் கணத்தாக்கு (J) ன் மதிப்பு, விசை மற்றும் கால அளவின் பெருக்கற் பலனுக்கு சமமாக இருக்கும்.

கணத்தாக்கு J = F x t

நியூட்டனின் இரண்டாவது இயக்க விதிப்படி

F = Δp/t (Δp என்பது t கால இடைவெளியில் ஏற்படும் உந்தமாற்றம் என்பதை குறிக்கிறது).

Δp = F x t

இரண்டு சமன்பாடுகளையும் சமன் செய்ய கணத்தாக்கு J = Δp

கணத்தாக்கு என்பது உந்த மாறுபாட்டிற்கு சமமான அளவாகும். இதன் அலகு கிகி மீவி^-1 அல்லது நியூட்டன் விநாடி அகும்.

உந்த மாற்றம் அல்லது கணத்தாக்கு கீழ்க்கண்ட இரு வழிகளில் செயல்படலாம்.

1. பொருளின் மோதல் காலம் குறையும் போது அப்பொருளின் மீது செயல்படும் கணத்தாக்கு விசையின் மதிப்பு அதிகமாகும்.
2. பொருளின் மோதல் கால மதிப்பு அதிகமாகும் போது அப்பொருளின் மீது செயல்படும் கணத்தாக்க விசையின் மதிப்பு குறையும்.

சில எடுத்துக்காட்டுகள்:

• சீரற்ற பரப்பில் இருச்சகக்கர வாகன பயணத்தின் போது கணத்தாக்கு விசை அதிர்வுகளை குறைப்பதற்கு சுருள்வில் அமைப்புகளும் அதிர்வுறிஞ்சிகளும் வைக்கப்ட்டுள்ளன.
• கிரிக்கெட் விளையாட்டில், வேகமாக வரும் பந்தினை பிடிக்க, விளையாட்டு வீரர் கையினை பின்னோக்கி இழுத்து மோதல் காலத்தை அதிகரிக்கிறார். இது அவரது கையில், பந்து ஏற்படுத்தும் கணத்தாக்கு விசையின் அளவை குறைக்கிறது.

கணத்தாக்கு:

மிக அதிக விசை, மிகக்குறுகிய நேரத்திற்கு ஒரு பொருளின் மீது செயல்பட்டால் அவ்விசையை கணத்தாக்கு விசை அல்லது கணத்தாக்கு என்று அழைக்கலாம்.

F என்ற விசை, மிகக் குறுகிய நேர இடைவெளியில் (Δt) ஒரு பொருளின் மீது செயல்பட்டால் நியூட்டன் இரண்டாம் விதியின் எண் மதிப்பு வடிவில் இந்நிகழ்வினை பின்வருமாறு குறிப்பிடலாம்.

எடுத்துக்காட்டுகள்:

1. கிரிக்கெட் வீரர், வேகமாகவரும் பந்தினை பிடிக்கும்போது அவரின் கரங்களை பந்து வரும் திசையிலேயே படிப்படியாக தாழ்த்துவதன் காரணம் என்ன?

கிரிக்கெட் வீரர் பந்தைப்பிடித்த உடன் தன்னுடைய கரங்களை தாழ்த்தாமல் உடனடியாக நிறுத்தினால் பந்து உடனடியாக ஓய்வுநிலைக்கு வரும். அதாவது பந்தின் உந்தம் உடனடியாக சுழியாகிறது. இதனால் கரங்களின் மீது பந்து செலுத்தும் சராசரி விசை பெரும் மதிப்பைப் பெறும். எனவே கிரிக்கெட் வீரரின் கரங்கள் வேகமாக தாக்கப்பட்டு அவர் அதிக வலியினை உணர்வார். இதனைத் தவிர்ப்பதற்காகத்தான் அவர் தன்னுடைய கரங்களை படிப்படியாக தாழ்த்துகிறார்.

2. வேகமாகச் செல்லும் கார் ஒன்று விபத்திற்குள்ளாகும்போது அதன் உந்தம் மிகக்குறைந்த நேரத்தில் மிக வேகமாகக் குறைகிறது. இது பயணிகளுக்கு பேராபத்தை விளைவிக்கும். ஏனெனில் பயணிகளின் மீது இவ்வுந்த மாற்றம் பெரும விசையினைச் செலுத்தும். மரணத்தை ஏற்படுத்தும் இந்த விளைவிலிருந்து பயணிகளைக் காக்க காற்றுப்பைகளுடன் கார்கள் தற்போது வடிவமைக்கப்படுகின்றன. இந்தக் காற்றுப்பைகள் பயணிகளின் உந்த மாற்றக் காலத்தை நீட்டித்து அவர்கள் பெரும் விசையைப்பெறுவதிலிருந்து தடுக்கிறது.
3. இரு சக்கர வாகனங்களில் பொருத்தப்பட்டுள்ள அதிர்வுத்தாங்கிகள் (Shock absorbers): கார்களில் உள்ள காற்றுப்பைகள் போன்றே இவையும் அதிர்வுதாங்கிகளாக செயலாற்றுகின்றன. மேடுபள்ளங்களில் வாகனம் செல்லும் போது ஒரு திடீர் விசையானது உடனடியாகவாகனத்தின்மீதுசெலுத்தப்படுகிறது. இவ்விசை பயணிகளை உடனடியாகத் தாக்காமல் அதன் தாக்குதல் நேரத்தை நீட்டிக்க அதிர்வுத்தாங்கிகள் பயன்படுகின்றன. எனவே பயணிகள் பெருமவிசையை உணர்வதிலிருந்து தடுக்கப்படுகின்றனர். அதிர்வுத்தாங்கிகள் சரிவர இயங்காத வாகனங்களில் பயணம் செய்வது நமது உடலை பாதிக்கும்.

மணல் நிரப்பிய தரையில் குதிப்பதைவிட, கான்கிரீட் தரையில் குதிப்பது பேராபத்தை விளைவிக்கும். ஏனெனில், மணல் நிரப்பப்பட்ட தரை நமது உடல் ஓய்வு நிலையை அடையும் நேரத்தை நீடித்து உடல் பெரும விசையைப் பெறுவதிலிருந்து தடுக்கும். ஆனால் கான்கிரீட் தளத்தில் குதிக்கும் போது உடல் உடனடியாக ஓய்வு நிலைக்கு வந்து ஒரு பெரும விசையை உணரும். இது பேராபத்தை விளைவிக்கும்.

ராக்கெட் ஏவுதல் நிகழ்வின்தத்துவம்:

ராக்கெட் ஏவுதலில் நியூட்டனின் மூன்றாம் விதி மற்றும் நேர்க்கோட்டு உந்த அழிவின்மை விதி, இவை இரண்டும் பயன்படுகின்றன. ராக்கெட்டுகளில் உந்து கலனில் (propellant tank) எரிபொருள்கள் (திரவ அல்லது திட) நிரப்பப்படுகின்றன. அவை எரியூட்டப்பட்டதும், வெப்ப வாயுக்கள் ராக்கெட்டின் வால் பகுதியில் இருந்து அதிக திசைவேகத்தில் வெளியேறுகின்றன.

அவை மிக அதிக உந்தத்தை உருவாக்குகின்றன. இந்த உந்தத்தை சமன் செய்ய, அதற்கு சமமான எதிர் உந்துவிசை எரிகூடத்தில் (combustion chamber) உருவாகி, ராக்கெட் மிகுந்த வேகத்துடன் முன்னோக்கி பாய்கிறது.

ராக்கெட் உயர பயணிக்கும் போது அதில் உள்ள எரிபொருள் முழுவதும் எரியும்வரை அதன் நிறை படிப்படியாக குறைகிறது. உந்த அழிவின்மை விதியின் படி நிறை குறைய குறைய, அதன் திசைவேகம் படிப்படியாக அதிகரிக்கிறது.

ஒரு குறிப்பிட்ட உயரத்தில் ராக்கெட்டானது புவியின் ஈர்ப்பு விசையினை தவிர்த்து விட்டு செல்லும் வகையில், அதன் திசைவேக மதிப்பு உச்சத்தை அடைகிறது. இது விடுபடு வேகம் (escape speed) எனப்படுகிறது.

நியூட்டனின் பொது ஈர்ப்பியல் விதி மற்றும் பயன்பாடுகள்:

அண்டத்தில் உள்ள பொருட்களின் ஒவ்வோர் துகளும் பிற துகளை ஒரு குறிப்பிட்ட விசை மதிப்பில் ஈர்க்கிறது. அவ்விசையானது அவைகளின் நிறைகளின் பெருக்கற்பலனுக்கு நேர்விகிதத்திலும், அவைகளின் மையங்களுக்கிடையே உள்ள தொலைவின் இருமடிக்கு எதிர்விகிதத்திலும் இருக்கும். மேலும் இவ்விசை நிறைகளின் இணைப்புக் கோட்டின் வழியே செயல்படும்.

இவ்விசை எப்போதும் ஈர்ப்பு விசையாகும். இவ்விசை, நிறைகள் அமைந்துள்ள ஊடகத்தை சார்ந்தது அல்ல.

m₁ மற்றும் m₂ என்ற நிறையுடைய இரு பொருள்கள் r என்ற தொலைவில் வைக்கப்பட்டுள்ளதாக கருதுவோம். இவற்றிற்கிடையே உள்ள ஈர்ப்பு விசை F ஆனது, பொது ஈர்ப்பியல் விதிப்படி

F ∝ m₁ × m₂

F ∝ 1/ r ²

இவை இரண்டையும் இணைத்து

G என்பது ஈர்ப்பியல் மாறிலி. இதன் மதிப்பு (SI அலகுகளில்) 6.674 x 10^-11 N m² kg^-2

புவிஈர்ப்பு முடுக்கம் (g)

பொருளொன்றை மேல்நோக்கி வீசினால் புவி ஈர்ப்பு விசையின் தாக்கத்தால், அதன் திசைவேகம் படிப்படியாக குறையும். ஒரு குறிப்பிட்ட உயரத்தில் அம்மதிப்பு முழுமையாக சுழி ஆகிறது. ஈர்ப்பு விசையினால் கீழே விழும் போது அதன் திசைவேகம் தொடர்ந்து மாற்றம் பெறுகிறது. இது அப்பொருளுக்கு முடுக்கத்தினை ஏற்படுத்தும். இம்முடுக்கம் புவி ஈர்ப்பு விசையினால் ஏற்படுவதால் புவிஈர்ப்பு முடுக்கம் என்றழைக்கப்படுகிறது.

புவி ஈர்ப்பு முடுக்கத்தின் சராசரி மதிப்பு (கடல் மட்டத்தில்) 9.8 மீ வி^-2 ஆகும். இதன் பொருளானது, தடையின்றி கீழே விழும் பொருளின் திசைவேகம், ஒரு வினாடிக்கு 9.8 மீ வி^-1 என்ற அளவில் மாற்றம் பெறும் என்பதாகும். g இன் மதிப்பு புவியில் அனைத்து இடங்களிலும் ஒரே மதிப்பாய் இருக்காது.

நியூட்டனின் ஈர்ப்பியல் விதியின் பயன்பாடுகள்:

1. அண்டத்தில் உள்ள விண்பொருட்களின் பரிமாணங்களை அளவிட பொது ஈர்ப்பியல் விதி பயன்படுகிறது. புவியின் நிறை, ஆரம், புவி ஈர்ப்பு முடுக்கம் முதலியனவற்றை துல்லியமாக கணக்கிட இவ்விதி உதவுகிறது.
2. புதிய விண்மீன்கள் மற்றும் கோள்களை கண்டுபிடிக்க இவ்விதி உதவுகிறது.
3. சில நேரங்களில் விண்மீன்களின் சீரற்ற நகர்வு (Wobble) அருகில் உள்ள கோள்களின் இயக்கத்தை பாதிக்கும். அந்நேரங்கள் அவ்விண்மீன்களின் நிறையினை அளவிட இவ்விதி பயன்படுகிறது.
4. தாவரங்களின் வேர் முளைத்தல் மற்றும் வளர்ச்சி புவியின் ஈர்ப்புவிசை சார்ந்து அமைவது ‘புவிதிசை சார்பியக்கம்’ என்றழைக்கப்படுகிறது. இந்நிகழ்வை விளக்க இவ்விதி பயன்படுகிறது.
5. விண்பொருட்களின் பாதையினை வரையறை செய்வதற்க்கு இவ்விதி பயன்படுகிறது.

g மற்றும் G இவற்றிற்கிடையே உள்ள தொடர்பு:

m என்ற நிறையுள்ள பொருள் ஒன்று ஓய்வு நிலையில் புவி பரப்பின் மீது உள்ளது. பொருளின் மீது செயல்படும் இரு விசைகளை கீழ் கண்டவாறு கணக்கிடலாம். M என்பது புவியின் நிறையாக கொள்வோம். புவியின் நிறை புவி மையத்தில் குவிந்திருப்பதாக எடுத்துக் கொள்வோம். புவியின் ஆரம் R = 6378 கி. மீ (தோராயமாக = 6400 கி. மீ) ஆகும்.

நியூட்டனின் பொது ஈர்ப்பியல் விதிப்படி, புவிக்கும் பொருளுக்கும் உள்ள ஈர்ப்பு விசை

இதே போல் பொருள் மீது செயல்படும் விசை மதிப்பை நியூட்டனின் இரண்டாம் விதிப்படி கணக்கிடலாம். இவ்விதிப்படி விசையானது பொருளின் நிறைக்கும், முடுக்கத்திற்கும் உள்ள

பெருக்கற்பலனாகும். இங்கு பொருளின் முடுக்கம், புவியின் ஈர்ப்பு முடுக்கத்திற்கு சமமாக இருப்பதால் (a = g)

F= ma = mg (எடை)

சமன்பாடுகளை சமன் செய்ய

இவற்றை சமன் செய்ய

mg = GMm / R²

எனவே புவி ஈர்ப்பு முடுக்கம்

g= GM / R²

இச்சமன்பாடு ‘g’ மற்றும் ‘G’ இவற்றிற்கிடையே உள்ள தொடர்பினை அளிக்கிறது.

புவியின் நிறை (M)

புவியின் நிறை M = g R² /G,

g, R மற்றும் G ன் மதிப்புகளை பிரதியிட புவியின் நிறை மதிப்பு M = 5.972 x 10²⁴ கிகி எனக் கணக்கிடப்படுகிறது.

புவி ஈர்ப்பு முடுக்க மாற்றம்:

புவிஈர்ப்பு முடுக்கம் g ன் மதிப்பு பூமியின் ஆரத்தை சார்ந்து அமையும். (g ∝ 1/R²) புவியின் ஆரம் நிலநடுக்கோட்டுப் பகுதியில் அதிகமாக உள்ளதால், ஈர்ப்பு முடுக்கத்தின் மதிப்பு குறைவாக இருக்கும். துருவப் பகுதியில் ஆர மதிப்பு குறைவாக உள்ளதால், ஈர்ப்பு முடுக்கம் அதிகமாக இருக்கும்.

நாம் புவியின் தரைப்பகுதியில் இருந்து உயரச் செல்லச் செல்ல புவி ஈர்ப்பு முடுக்கம் படிப்படியாக குறையும். அதேபோல் புவியின் அடி ஆழத்திற்கு செல்லச் செல்ல புவிஈர்ப்பு முடுக்கத்தின் மதிப்பு குறைகிறது. புவியின் மையத்தில் ‘g’ ன் மதிப்பு சுழியாகும்.

நிறை மற்றும் எடை வேறுபாடு:

நிறை: நிறை என்பது பொருட்களின் அடிப்படை பண்பாகும். பொருட்களின் நிறை என்பது அதில் அடங்கியுள்ள பருப்பொருளின் அளவாகும். இதன் அலகு கிலோகிராம் ஆகும்.

எடை: ஒரு பொருளின் மீது செயல்படும் ஈர்ப்பு விசையின் மதிப்பு அப்பொருளின் எடை என்றழைக்கப்படுகிறது.

எடை W = நிறை (m) x புவி ஈர்ப்பு முடுக்கம் (g)

எடை ஓர் வெக்டார் அளவாகும். அது எப்போதும் புவியின்மையத்தை நோக்கி செயல்படும். அதன் அலகு நியூட்டன் (N). எடையானது புவிஈர்ப்பு முடுக்கத்தைச் சார்ந்தது. புவிஈர்ப்பு முடுக்கமதிப்பு புவியில் இடத்திற்கு இடம் மாறுபடுவதால், எடையின் மதிப்பும் இடத்திற்கு இடம் மாறுபடும். பொருட்களின் எடை துருவப்பகுதியில் அதிகமாகவும், நிலநடுக்கோட்டுப் பகுதியில் குறைவாக இருக்கும்.

நிலவில் ஈர்ப்பு முடுக்கத்தின் மதிப்பு 1.625 மீவி^-2 ஆகும். இது புவியின், ஈர்ப்பு முடுக்கத்தில் 0.1654 மடங்கிற்கு சமமான அளவாகும். 60 கிகி நிறையுள்ள ஒருவர் பூமியில் 588N எடையுடன் (W=mg=60 x 9.8 = 588N) நிலவில் 97.5N (W = mg = 60 x 1.625 = 97.5N) எடையுடன் இருப்பார். ஆனால் அவரது நிறை மதிப்பு (60 kg) புவியிலும் நிலவிலும் மாறாது இருக்கும்.

விண்வெளி வீரரின் எடையிழப்பு:

புவியினைச் சுற்றிவரும் விண்கலனில் வேலை செய்யும் விண்வெளிவீரர், அங்கு புவி ஈர்ப்பு விசை இல்லாததாலேயே மிதக்கிறார் என நாம் நினைக்கிறோம். இது தவறான கூற்றாகும்.

விண்வெளி வீரர் உண்மையில் மிதப்பதில்லை. விண்கலம் மிக அதிக சுற்றியக்க திசைவேகத்தில் நகர்ந்து கொண்டிருக்கிறது. அவர் அக்கலத்துடன் இணைந்து சம வேகத்தில் நகர்கிறார். அவரது முடுக்கம், விண்கல முடுக்கத்திற்கு சமமாக இருப்பதால், அவர் ‘தடையின்றி விழும் நிலையில் (free fall) உள்ளார். அப்போது அவரது தோற்ற எடை மதிப்பு சுழியாகும். எனவே அவர் அக்கலத்துடன் எடையற்ற நிலையில் காணப்படுகிறார்.

இரவு பகல் இரு வேளைகளிலும் சூரியனைப் பொறுத்து நாம் ஒரே வேகத்தில் செல்கிறோமா:

புவி, சூரியனை நீள்வட்டப்பாதையில் சுற்றி வருகிறது. சூரியனைப்பொறுத்து புவிமையத்தின் திசைவேகத்தை என்க. இந்த  சூரியனைப் பொறுத்து புவி நீள்வட்டப்பாதையில் சுற்றி வருவதால் ஏற்படுகிறது. அதே நேரத்தில் புவி தன் அச்சினைப் பொறுத்து தற்சுழற்சி இயக்கத்தை மேற்கொள்கிறது. புவியின் மேற்பரப்பில் உள்ள அனைத்துப் பொருட்களும் புவியின் தற்சுழற்சி அச்சினை மையமாகக் கொண்டு  என்ற திசைவேகத்தில் வட்டப்பாதை இயக்கத்தை மேற்கொள்கின்றன.

இரவு நேரங்களில்  மற்றும்  இரண்டும் ஒரே திசையில் அல்லது ஒன்றுக்கொன்று குறுங்கோண வேறுபாட்டு திசையில் செயல்படுகின்றன. எனவே, இரவில் சூரியனைப்பொருத்து புவியின் மேற்பரப்பில் உள்ள பொருளின் திசைவேகம்  ஆகும். ஆனால் பகல் நேரங்களில்  மற்றும்  இரண்டும் ஒன்றுக்கொன்று எதிர்திசையில் அல்லது விரிகோண வேறுபாட்டு திசையில் செயல்படுகின்றன.

எனவே, பகற்பொழுதில் சூரியனைப் பொறுத்து புவிப்பரப்பில் உள்ள பொருட்களின் திசைவேகம்  ஆகும். இதிலிருந்து புவியின் பரப்பில் எந்த ஒரு பொருளும் பகலைவிட இரவு நேரத்தில் சூரியனைப் பொறுத்து வேகமாகச் செல்லும் என அறியலாம். இது புவியின் சுழற்சியால் ஏற்படுகிறது. இதனை பின்வரும் படத்தின் மூலம் அறியலாம்.

மையநோக்கு விசை மற்றும் மையவிலக்கு விசை:

துகளொன்று சீரான வட்டப்பாதையில் சுற்றி வரும்போது வட்டமையத்தை நோக்கி வட்டப்பாதையின் ஆரம் வழியாக மையநோக்கு முடுக்கம் ஏற்படும். நியூட்டனின் இரண்டாம் விதிப்படி முடுக்கம் ஏற்பட்டால் நிலைமக் குறிப்பாயத்தைப் பொருத்து துகளின்மீது ஒரு விசை செயல்பட வேண்டும். அவ்வாறு துகளின் மீது செயல்படும் விசையே மையநோக்கு விசை எனப்படும்.

• மெல்லிய கயிற்றின் ஒரு முனையில் கட்டி சுழற்றப்படும் கல்லின் இயக்கத்தில், கயிற்றின் இழுவிசையே மையநோக்கு விசையாகச் செயல்படுகிறது. பொழுதுபோக்குப் பூங்காக்களில் இயக்கப்படும் இராட்டினம் போன்ற சுழற்சி இயக்கத்தில், இராட்டினத்தைத் தாங்கும் இரும்புக் கம்பிகளின் இழுவிசை மையநோக்கு விசையை அளிக்கிறது.
• புவியினைச் சுற்றி வரும் செயற்கைக் கோளின் இயக்கத்தில், புவி, செயற்கைக் கோளின் மீது செலுத்தும் புவியீர்ப்பு விசையே மையநோக்கு விசையாகச் செயல்படுகிறது. செயற்கைக்கோள் இயக்கத்திற்கு நியூட்டனின் இரண்டாம் விதியை கீழ்காணுமாறு எழுதலாம்
  

இங்கு r என்பது புவியின் மையத்திலிருந்து செயற்கைக்கோள் உள்ள தொலைவு

• கார் ஒன்று வட்டவடிவப்பாதையில் செல்லும்போது, மையநோக்கு விசையானது காரின் டயருக்கும், சாலைக்கும் இடையே ஏற்படும் உராய்வு விசையினால் ஏற்படுகிறது.
  

கார்வளைவுப் பாதையில் செல்லும் போதும், மையநோக்கு விசையைப் பெறுகிறது. காரின் டயருக்கும், சாலைக்கும் இடையே ஏற்படும் உராய்வு விசையினால் இம்மையநோக்கு விசை ஏற்படுகிறது.

• கோள்கள் சூரியனைச் சுற்றி வரும்போது, அவை சூரியனின் மையத்தை நோக்கிய, ஒரு மையநோக்கு விசையைப் பெறுகின்றன. இங்கு கோள்களின் மீதான சூரியனின் ஈர்ப்பு விசை, மையநோக்கு விசையாகச் செயல்படுகிறது.

இந்நிகழ்விற்கான நியூட்டனின் இரண்டாம் விதியை பின்வருமாறு எழுதலாம்

கோள்களின் மீது சூரியனின் ஈர்ப்புவிசை = mv² / r²

மையவிலக்கு விசை

சுழற்சிக் குறிப்பாயத்தைப் பொருத்து, வட்டமையத்தை நோக்கிச் செயல்படும் மையநோக்கு விசையான -mω²r உடன், அதற்குச் சமமான எதிர்திசையில் வெளிநோக்கிச் செயல்படும் + mω²r என்ற விசை கல்லின் மீது செயல்படுகிறது. எனவே சுழற்சி இயக்கத்திலுள்ள குறிப்பாயத்தைப்பொருத்து கல்லின் மீது செயல்படும் தொகுபயன் விசை சுழியாகும் என்பதை இது காட்டுகிறது. (-mω²r + mω²r = 0) இங்கு வெளிநோக்கிச்செயல்படும் + mω²r விசைக்கு மையவிலக்கு விசை என்று பெயர்.

மைய விலக்கு விசையின் விளைவுகள்:

மையவிலக்கு விசை ஒரு போலியான விசையாக இருப்பினும் அதன் விளைவுகள் உண்மையாகும். கார் ஒன்று வளைவுப்பாதையில் திரும்பும்போது, காரின் உள்ளே அமர்ந்திருப்பவர் ஒரு வெளிப்புறவிசையை உணர்வார். அவ்விசை அவரை வெளிநோக்கித் தள்ளும்.

இவ்வெளிநோக்கிய விசையையும் மையவிலக்கு விசைஎன்றே அழைக்கலாம். காரின் இருக்கைக்கும், அமர்ந்திருக்கும் நபருக்கும் இடையே உள்ள போது மான உராய்வுவிசை இருந்தால் அவர் வெளியே தள்ளப்படுவது தவிர்க்கப் படுகிறது.

நேர்க்கோட்டுப் பாதையில் சென்று கொண்டிருக்கும் கார் ஒன்று திடீரென்று தன்பாதையிலிருந்து வளையும்போது, காரின் உள்ளே நிலையாகப் பொருத்தப்படாத பொருள், திசையில் நிலைமப் பண்பின் (Inertiaofdirection) காரணமாகநேர்க்கோட்டுப் பாதையிலேயே தொடர்ந்து இயங்க முயற்சிக்கும்.

இவ்வியக்கத்தை நிலைமக் குறிப்பாயத்திலிருந்து பார்க்கும் போது நேர்கோட்டு இயக்கமாகத் தெரியும். ஆனால் சுழற்சிக் குறிப்பாயத்திலிருந்து பார்க்கும்போது இயக்கம் வெளிநோக்கிச் செல்வது போன்று தோன்றும்.

சுழலும் மேடையில் நின்று கொண்டிருக்கும் நபர் வெளிப்புற மையவிலக்கு விசையை உணர்வார். இதன் காரணமாக மேடையிலிருந்து அவர் வெளியே தள்ளப்பட வாய்ப்பு அதிகம். நின்று கொண்டிருக்கும் நபருக்கும், மேடைக்குமான உராய்வுவிசை வெளிநோக்கித் தள்ளப்படும் விசையினைச் சமன் செய்யப் போதுமானதல்ல.

இதனைத் தவிர்ப்பதற்காக மேடையின் வெளிப்புற விளிம்பு சற்றே மேல்நோக்கி உயர்த்தப்பட்டிருக்கும். இவ் உயர்வு நின்று கொண்டிருக்கும் நபரின் மீது ஒரு செங்குத்து விசையைச் செலுத்தி அவர் வெளியே விழுவதைத் தடுக்கும்.

சரி சமமான வட்டச் சாலையில் செல்லும் வாகனத்தின் இயக்கம்:

வாகனமொன்று வளைவுப்பாதையில் செல்லும் போது, அவ்வாகனத்தின் மீது மையநோக்கு விசை செயல்படுகிறது. வாகனத்தின் டயர் மற்றும் சாலையின் மேற்பரப்பு இவற்றிற்கிடையேயான உராய்வு விசையின் காரணமாக இம்மையநோக்குவிசை ஏற்படுகிறது. m நிறையுடைய வாகனமொன்று r ஆரமுடைய வட்டவடிவப் பாதையில் v வேகத்தில் இயங்குகிறது எனில், அவ்வாகனத்தின் மீது மூன்று விசைகள் செயல்படுகின்றன.

• கீழ்நோக்கிச் செயல்படும் புவிஈர்ப்புவிசை (mg)
• மேல்நோக்கிச் செயல்படும் செங்குத்துவிசை N
  
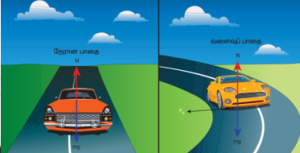
• சாலையின் கிடைத்தளப் பரப்பின் வழியே உள்நோக்கிச் செயல்படும் உராய்வு விசை (F_S)

சாலை கிடைத்தளமாக இருப்பின், செங்குத்து விசையும், புவியீர்ப்பு விசையும் ஒன்றுக்கொன்று சமம் மற்றும் எதிரெதிராக இருக்கும். வாகனத்தின் டயருக்கும், சாலையின் பரப்பிற்கும் இடையே ஏற்படும் உராய்வுவிசைதேவையானமையநோக்கு விசையை அளிக்கிறது. இம்மையநோக்கு விசை வட்டச்சாலையின் மையத்தை நோக்கிச் செயல்படுகிறது.

நாம் முற்பகுதியில் கற்றபடி, நிலை உராய்வுவிசை சுழி முதல் பெரும் மதிப்பு விசை வரை எந்த மதிப்பையும் பெறலாம். எனவே இங்கு இரண்டு நிபந்தனைகள் சாத்தியமாகிறது:

வளைவுச்சாலையில், வாகனம் வளைவதற்குத் தேவையான மையநோக்கு விசையை நிலை உராய்வு கொடுக்கிறது. எனவே வாகனத்தின் டயர் மற்றும் சாலையின் பரப்பு இவற்றிற்கிடையேயான நிலை உராய்வுக் குணகம் வாகனம் சறுக்காமல் வளைவுப்பாதையில் வளைவதற்கான பெருமவேகத்தை நிர்ணயிக்கிறது.

வாகனம் வளைவதற்குத் தேவையான மையநோக்கு விசையை நிலை உராய்வுவிசையினால் கொடுக்க இயலவில்லை எனில், வாகனம் சறுக்கத் தொடங்கும்.

சாலையின் வெளிவிளிம்பு உயர்த்தப்பட காரணம்:

சரிசமமான வட்டச் சாலையில், வாகனங்கள் சறுக்கி விபத்துக்குள்ளாவது, சாலைப் பரப்பின் நிலை உராய்வு குணகத்தை சார்ந்திருக்கிறது. இந்த நிலை உராய்வுக் குணகத்தின் பெரும் மதிப்பு பரப்பின் தன்மையைச் சார்ந்ததாகும்.

இதன் காரணமாக வாகனங்களுக்கு ஏற்படும் விபத்தினைத் தடுப்பதற்காகச் சாலையின் வெளிவிளிம்பு உட்புற விளிம்பை விட சற்றே உயர்த்தி அமைக்கப்பட்டிருக்கும். இதற்கு வெளிவிளிம்பு உயர்த்தப்பட்ட சாலை (banking of tracks) என்று பெயர். வெளிவிளிம்பு உயர்த்தப்பட்டிருப்பதால் இது ஒரு சாய்தளம் போன்று அமையும். கிடைத்தளப் பரப்புடன் இந்தச் சாய்தளம் ஏற்படுத்தும் கோணம் வெளிவிளிம்புக்கோணம் (bankingangle) எனப்படும்.

கிடைத்தளத்துடன் θகோணத்தில் உள்ள சாலையின் பரப்பைக் கருதுக. செங்குத்துவிசை, செங்குத்து அச்சுடன் இதே θ கோணத்தை ஏற்படுத்தும். இச்சாலையில் செல்லும் கார் ஒன்று வளையும்போது அதன் மீது இரண்டு விசைகள் செயல்படும்.

1. கீழ்நோக்கிச் செயல்படும் புவியீர்ப்பு விசை (mg)
2. சாலையின் பரப்பிற்குச் செங்குத்தாகச் செயல்படும் செங்குத்து விசை (N)

செங்குத்து விசை N ஐ இரண்டு கூறுகளாகப் பிரிக்கலாம். இவை N cosθ மற்றும் Nsinθ ஆகும். N cosθ கூறு, கீழ்நோக்கிச் செயல்படும் புவியிர்ப்பு விசையை (mg) சமன் செய்கிறது. Nsinθ கூறு தேவையான மையநோக்கு விசையைக் கொடுக்கிறது.

நியூட்டனின் இரண்டாம் விதியைப் பயன்படுத்தி பின்வரும் சமன்பாடுகளை அமைக்கலாம்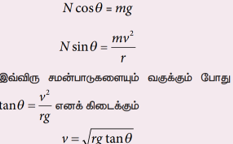

வெளி விளிம்புக் கோணம் மற்றும் சாலையின் வளைவு ஆரம் (r) இவ்விரண்டும் வளைவுச் சாலையில் பாதுகாப்பாக வாகனங்களை இயக்க வேண்டிய வேகத்தைத் (v) தீர்மானிக்கின்றன. வாகனம் ஒன்றின் வேகம் நிர்ணயிக்கப்பட்ட வேகத்தைவிட அதிக வேகத்தில் செல்லும் போது சாலையின் வெளிப்புறத்தை நோக்கி சறுக்கத் தொடங்கும்.

ஆனால் உராய்வு விசை செயல்பட்டு கூடுதல் மையநோக்கு விசையினைக் கொடுத்து வெளிப்புறச் சறுக்குதலைத் தடுக்கும். அதே நேரத்தில் காரின் வேகம் நிர்ணயிக்கப்பட்ட வேகத்தை விட குறைவாக இருப்பின் கார் உட்புறத்தை நோக்கி நகரத் தொடங்கும்.

உராய்வு விசை செயல்பட்டு மையநோக்கு விசையைக் குறைத்து உட்புறத்தை நோக்கி சறுக்குவதைத் தடுக்கும். இருப்பினும் காரின் வேகம் மிக அதிகம் எனில் உராய்வு விசையினால் கார் சறுக்குவதைத் தடுக்க முடியாது.